勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

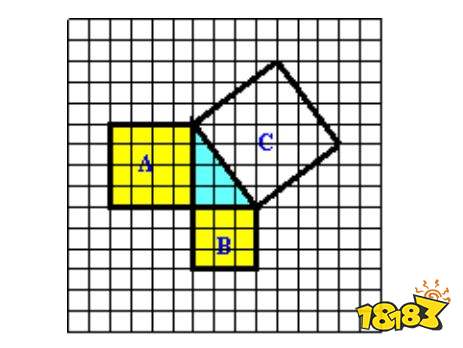
勾股定理的概念和公式

勾股定理公式表a^2+b^2=c^2

勾股定理的概念：

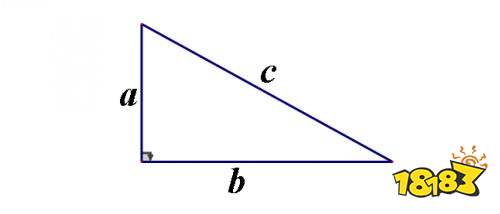
勾股定理指的是：直角三角形两直角边的平方和等于斜边的平方。如下图。

勾股定理的概念和公式

勾股定理在中国的起源：

我国最早的数学著作《周髀算经》中记载着一段周公向商高请教数学知识的对话：周公问：“天没有梯子可以上去，地也没法用尺子去一段一段丈量，那么怎样才能得到关于天地的数据呢?”商高回答说：“数据根据圆和方的道理得来的，圆从方来，方又从矩来。这里的“矩”原是指给直角的作图工具，可能就是一个长方形：当直角三角形‘矩’得到的一条直边‘勾’等于3，另一条直角边‘股’等于4的时候，那么它的斜边‘弦’就必定是5。”这段文字体现了我国很早便发现和应用了勾股定理，并阐释出了勾股定理是借助于形来解决数的问题。

勾股定理在西方的发现：

勾股定理的概念和公式

勾股定理在西方称毕达哥拉斯定理。相传毕达哥拉斯有一次应邀参加一位富有的政要的晚餐会，这位主人豪华宫殿般的餐厅铺着美丽的正方形大理石地砖。善于观察的毕达哥拉斯凝视脚下这些方形磁砖，他不只是欣赏磁砖的美丽，而是想到它们和“数”之间的关系，于是拿了画笔蹲在地板上，选了一块磁砖以它的对角线为边画一个正方形，他发现这个正方形面积恰好等于两块磁砖的面积和。他很好奇，于是再以两块磁砖拼成的矩形之对角线作另一个正方形，他发现这个正方形之面积等于5块磁砖的面积，也就是以两股为边作正方形面积之和。至此毕达哥拉斯作了大胆的假设：任何直角三角形，其斜边的平方恰好等于另两边平方之和。

，